三角形 と 比 の 定理 の 逆

無 排卵 月経 おり もの 特徴「三角形の比の定理」とは？三角形の比の定理の逆の証明も . 三角形と比の定理の逆 三角形と比の定理っていうのは DE//BCならば、下の2つの比の関係が成り立つっていうものだったよね。 三角形と比の定理の逆っていうのは、さっきの矢印が逆になったバージョンのことだよ。今回は逆について考えて. 平行線と線分の比の問題・3通りの証明・定理の逆の証明を解説 . こんにちは、ウチダです。 今日は、中学3年生で習う 「平行線と線分の比の定理」 を用いる問題や、その $3$ 通りの証明、また定理の逆の証明について、わかりやすく解説していきます。 平行線と線分の比の定理とは【台形】 まずは. 【高校数学a】チェバの定理とその逆の証明 | 受験の月. 三角形の内角・外角の二等分線と辺の比の関係とその証明 三角形の面積比（等高, 等底, 等角） チェバの定理とその逆の証明 メネラウスの定理とその逆の証明 チェバの定理とメネラウスの定理の基本問題演習 三角形の五心① 三角形の. 線分比・相似の定理 - 中学校数学・学習サイト. 出産 手当 金 扶養 に 入っ て しまっ た

9 月 の 恋 と 出会う まで あらすじ ネタバレ三角形と比の定理 A B C D E ABCの辺AB,AC上の点をそれぞれD, Eとするとき、 ①DE//BCならAD:AB=AE:AC=DE:BCである。 ②DE//BCならAD:DB=AE:ECである。 ※この定理はD, Eが辺BA, CAの延長上にあっても成り立つ。 定理の証明 【例】それぞれBC//DEである。 8cm 6cm 9cm 7cm x y A B C D E BC//DEより BC:DE=AC:AE=AB:AD 8:6=x:9 6x=72 x=12 8:6=7:y 8y=42 y= 21 4 A B C D E 6cm 4cm 9cm 8cm x y BC//DEよりAE:AC=DE:BC 6:10=9:x 6x=90 x=15 BC//DEよりAE:EC=AD:DB. 「三角形の比の定理」とは？ 三角形の比の定理の逆の証明も . 【現在閲覧中】「三角形の比の定理」とは？ 三角形の比の定理の逆の証明も解説 「中点連結定理」とは？ 三角形の中点連結定理の証明をわかりやすく解説 平行線と線分の比をわかりやすく解説 （相似・平行線と比の定理）.

2021 3学年 5章 2節 平行線と比②〜三角形と比の定理の逆 . 三角形と比の定理の逆です。 ABCで、 ①AD:AB=AE:ACならばDE//BC .more .more 三角形と比の定理の逆です。 ABCで、①AD:AB=AE:ACならばDE//BC②AD:DB=AE:EC ならばDE//BCが成り立ちます。. 【超わかる授業動画「相似な図形」】第25回 三角形と比の定理 . 今回は前回紹介した三角形と比の定理の「逆」の基本的な使い方を解説します。 平行になるための条件ですから、どのように図形を見て、クロワッサン型、もち型、チョウチョ型のそれぞれの逆のどれを使うのかを見極められるようにしましょう。 三角形と比の定理の逆をこのあるある問題で慣れていきましょう。 【YouTubeによる中学3年の. 平行線と線分の比をわかりやすく解説（相似・平行線と比の定理）. 三角形と比の定理 ①DE//BCならば AD:AB ＝ AE:AC ＝ DE:BC ②DE//BCならば AD:DB ＝ AE:EC では、上の図の ABCの「辺AC」を右に平行移動させてみるよ。 平行移動させただけだから AC＝AC、AE＝AE、EC＝EC になるよね。 ということは、「三角形の比の定理」で確認した AD:AB ＝ AE:AC ＝ DE:BC AD:DB ＝ AE:EC の「AC」「AE」「EC」それぞれ AC＝AC、AE＝AE、EC＝EC とすることができるのだから、 次のような性質が成り立つということになるんだ。. 動画で学習 - 2 三角形と比の定理の逆 | 数学 - SchoolTV. 三角形と比の定理の逆とその証明- 小学生・中学生が勉強するならスクールTV。 全国の学校の教科書に対応した動画で学習できます。 授業の予習・復習にぴったり。. 中3数学/Vol.5-2-2【三角形と比の定理の逆①】暗記から理解に . 今回は中学3年生で学習する「三角形と比の定理の逆①」を解説しました! やはた塾とは？ 中学生で習う数学を分かり易く解説してYouTubeで提供し . チェバの定理の逆 | 三角形の内部で交わる1点をベクトルで表す . " チェバの定理の逆 "は高校数学の平面図形の単元で学習する内容になります。図形についての基本なだけに、ベクトルと合わせて議論を進めるということも考えられます。この記事では、三角形の内部のただ 1 点で交わった交点を位置ベクトルを用いて表すことを解説しています。.

動画で学習 - 1 三角形と比 | 数学 - SchoolTV. ・三角形と比の定理 ・三角形と比の定理を使って、線分の長さを求めること ・三角形と比の定理の逆 ・三角形と比の定理の逆を使って、平行な線分を見つけること ・三角形の角の二等分線の性質- 小学生・中学生が勉強するならスクールTV。全国. 5章：相似 | タカラゼミ. 相似な図形で対応する部分の長さの比を相似比といいます。例えば、相似な2つの円では、その相似比は半径の比と等しくなります。続いて三角形の相似条件についてですが、2つの三角形において (1) 3組の辺の比が全て等しい (2) 2組の辺の比とその間の角がそれぞれ等しい (3) 2組の角がそれぞれ . 三角形と比の定理の逆 - 全国中学高校Webコンテスト. 三角形と比の定理の逆 点D、E、F はを 4等分 するよう はを 4等分 するよう においてある。 線分DG、EH、FI は 線分BC とどのよ うな関係にあるだろうか？ 結論からいってしまうと 線分DG、EH、FI は 線分BC と平行に なっているんだ。 二つの辺をそれぞれ等しい辺にわけ て、それぞれ対応する 2点 を結んで できた線分は平行になるんだ。 クリック! まとめ! 三角形と比の定理の逆 ABC において、 点D、E をそれぞれ 辺AB、AC 上、また はその延長上の点とするとき次のことがいえる。 ①AD：AB＝AE：AC＝ならばDE//BC ②AD：DB＝AE：ECならばDE//BC この定理は下図のような場合も成り立つ!. 三角形と比の定理 - GeoGebra. 三角形と比の定理 作成者: Geo_Math_Room トピック: 平面図形や形, 相似三角形, 三角形 新しい教材 standingwave-reflection-free 斜めドップラー 正17角形 作図 regular 17-gon 2 目で見る立方体の2等分 直方体の対角線 教材を発見 . 三角比と三角関数の定義および公式 | 理数系学習サイト kori.

三平方の定理を使えば直角三角形の斜辺とその他の辺の長さの関係が分かるので、三角比の値を計算する事ができます。 30°、45°、60°の三角比の具体的な値は図形的な考察から導出する事ができて、整理すると次のようになります。. 10 図形の性質 | 教えて数学理科. (1)中学の復習(直線図形)(2)三角形の性質(2-1)角の二等分線の定理(2-2)角の二等分線の定理の逆(2-3)三角形の3辺の大小(2-4)三角形の辺と角の大小関係(2-5)中線定理(2-6)面積比(2-7)平面上の最短距離(2-8)折. PDF 2．三角形と比についての定理の逆. 1．三角形と比の定理の逆を次のように証明した。 空欄をうめなさい。 A ＜仮定＞ AD：DB＝AE：EC ＜結論＞ DE//BC ＜証明＞点Bを通り，辺CA に平行な直線と，ED を延長した 直線との交点をFとする（BF//AE－①）。. 【超わかる授業動画「相似な図形」】第26回 三角形と比の定理 . 今回は少し線が多い図において三角形と比の定理の「逆」の使い方を解説しています。 しっかりと文章や図の情報を頭の中で整理し、平行である線分と平行でない線分を確認することで、三角形と比の定理が使えるのかそうでないのか、三角形と比の定理の逆を使わなければならないのかを見極められるようにしましょう。 学習した知識を総合的に活. 博多 駅 金 の カエル

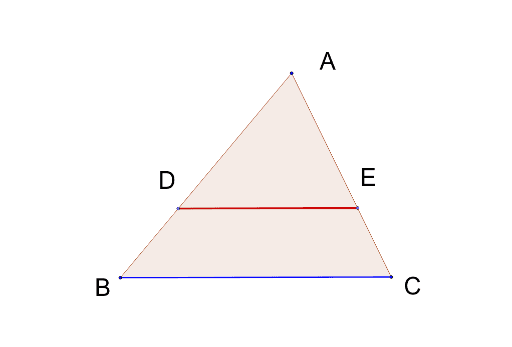
銀 歯 痛い 寝れ ない数学。三角形と平行線の線分の比。. 2 三角形と平行線の線分の比のルールの逆 2.1 1つ目のパターン 2.2 2つ目のパターン 3 まとめ 3.1 関連記事 三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。 ルールは 2つの図形のパターン について 覚えておきましょう!. 角の二等分線の定理：内分点・外分点での辺の比と証明問題 . 三角形の角の二等分線と辺の比には、内分と外分の2種類がある 高校数学では、三角形について内分点や外分点を利用して辺の比を計算します。特に、三角形の角の二等分線を利用します。このとき、以下の2つの定理を理解しましょう。. 三角関数 - Wikipedia. 鋭角を扱う場合、三角関数の値は対応する直角三角形の二辺の長さの比（三角比）である。 三角法に由来する 三角関数 という呼び名のほかに、 単位円 を用いた定義に由来する 円関数 （えんかんすう、 circular function ）という呼び名がある。. チェバの定理 - Wikipedia. チェバの定理はこの2つの式の比を計算することで導くことができる。 逆 チェバの定理の逆もまた成り立つ。即ち、任意の三角形ABCにおいて直線AB、BC、CA上に点D、E、Fをとり、D、E、Fのうち三角形ABCの辺上にある点が1個或いは. 数学メモ.115 三角形の最大角の問題, sinA: sinB: sinC. 数学メモ.115 三角形の最大角の問題, sinA: sinB: sinC. 高校数学の「三角比」の問題を解きます。. 平凡な解答例を書きました。. では、問題と解答例です。. ABCにおいて、sin A : sin B : sin C = 1 : sqrt 2 : sqrt 5 が成り立つとき、最も大きい角の大きさを求めよ。. ここ . 【中学3年数学/相似】145 三角形と比の定理の応用問題① . 4 Share 597 views 1 year ago （中3）相似 中学3年生数学で学習する、三角形と比の定理を利用して長さや比を求める応用問題です。 三角形と平行線が組み合わさると比がそろうこと、またその逆が成り立つことを利用して解いていきます。 プリントはダウンロードできますので、プリント ww.sugakuonline.com/print/. 三角形の面積の計算機 | ヘロンの公式より3辺から計算. 三角形の面積 (ヘロンの公式)の計算ツール. 本計算ツールは ヘロンの公式を使用して. 『三角形の3辺の長さ (a,b,c) から面積 S を求める』計算ツールです。. 【3辺の長さの入力】. a = b = c =. 【出力値の設定】. 出力値の小数点以下の桁数 : 3辺の. 長さ. 【高校数学i】三角形の内接円の半径と面積 ＃19 - 学校より . このページでは、 数学I「三角形の内接円の半径と面積」の問題を、わかりやすく解説していきます。. 問題集を解く際の参考にしてください!. 三角形の内接円の半径と面積【数I 三角比】#19. Watch on. 問題. 公式. 「円周角の定理の逆」とは？証明と問題の解き方をわかり . 今回学習する「円周角の定理の逆」は、今復習した2つの「円周角の定理」のうち、「1つの弧に対する円周角の大きさは一定である。 」という性質に注目していくよ。 ∠Pと∠Cの大きさを比べよう 下の図のように、点Pが円周の上にあると、 ∠APB＝∠ACB（∠C） になるよね。 まさにこれが「円周角の定理」の性質だよね。 つまり、「弧ABがあり、その円周角である∠Cと∠APBは同じ角度になる」ということだね。 ここで注目して欲しいのは、 「弧AB」ということは、「AとBはひとつの円の円周上」にある。 「円周角∠C」ということは、「cは、弧ABと同じ円の円周上」にある。 「円周角∠APB」ということは、「Pは、弧ABと同じ円の円周上」にある。. 数学メモ.113 三角形の辺と角の問題a=?,b=√2,c=2,∠B=30°. 余弦定理と「三角形の内角の和は180 」を使って、辺と角を求める問題。cos Aを計算しても有名角のcosの値にならないが、焦らず、cos Cを計算すると有名角が当てはまるのでよし。結びに一言。この解答例は、私が作成したごく平凡な. 余弦定理の計算機 | 三角形の辺の長さ、角度の計算. 余弦定理の計算ツール. 本計算ツールは 余弦定理 から 三角形の辺の長さ、角度を計算する計算機です。. 以下の ① または ② から、他の辺の長さと角度を求めます。. ・『 ① 2辺の長さ と 2辺の間の角度 』. ・『 ② 3辺の長さ 』. チェバの定理の逆とその証明-三角形の辺上の点が3つの場合と1つの場合・メネラウスの定理の逆との違い｜スライドで学ぶ高校数学 | ひまわり数学教室. 1．チェバの定理の逆. チェバの定理の逆. ABCにおいて，直線BC，CA，AB上にそれぞれ点P，Q，Rがあり，このうち1個または3個が辺上の点とする．このとき，BQとCRが交わり，かつ BP PC ⋅ CQ QA ⋅ AR RB = 1 B P P C ⋅ C Q Q A ⋅ A R R B = 1 ならば，3直線AP，BQ，CRは1点で . 中3相似「平行線と線分の比の逆」の証明 - YouTube. そして、いいねとチャンネル登録もしてくださっている皆様、本当に本当にありがとうございます! . です^^相似の「平行線と線分の比の逆」の . 中線定理とは？定理の証明や計算問題をわかりやすく解説! | 受験辞典. 生き ぼく ろ 除去

オーザック 消え たこの記事では、「中線定理」の意味や証明方法などを紹介していきます。. また問題の解き方もわかりやすく解説するので、ぜひマスターしてくださいね!. 目次 [ 非表示] 中線定理とは？. 例題「3 辺の長さから中線の長さを求める」. 中線定理の証明. 証明 . 【中学数学】中点連結定理 | 中学数学の無料オンライン学習サイトchu-su-. ただのピラミッド型じゃないですか・・・中点連結定理などという、たいそうな名前がついた定理ですが、以前 中学数学の基本から難問までの問題と分かりやすい解説を掲載した完全無料のオンライン学習ページです。. 中学数学3 平行線と線分の比の証明 - マナペディア. 平行線と線分の比 上図のように ABCにおいて、辺ABと辺AC上に点Pと点QがあってPQBC（平行）なとき、次の定理が成り立つ。 AP：PB＝AQ：QC このテキストでは、この定理を証明します。 証明 図のように、点Qを通ってPBと平行に. 円周角の定理の解説・問題の解き方｜数学FUN. 逆に、「直角三角形の各頂点を通る円は、斜辺（直角に対する辺）がその円の直径になる」というのも重要な性質です。 円周角の定理の逆 図のように 「点A、点B、点P、点Qにおいて、∠APQ＝∠AQBなら、すべての点は1つの円周上にある」 といえます。. 角の二等分線定理（内角、外角それぞれ） - 具体例で学ぶ数学. この問題をさらに発展させた有名な問題として、三角形の内心の証明と頻出例題2問の例題2があります。 外角バージョンとその証明. 外角の二等分線についても同様に辺の比に関する定理が成立します。. 接弦定理まとめ（証明・逆の証明） - 理系ラボ. 数学A2019.04.08. 接弦定理まとめ（証明・逆の証明）. 東大塾長の山田です。. このページでは、「接弦定理」について解説します。. 接弦定理とその証明を、イラスト付きで丁寧にわかりやすく解説していきます。. また、接弦定理の逆についても解説します .

平行線と線分の比の定理の逆は成り立たない反例を教えて下さい。 - 図を描. - Yahoo!知恵袋. 三角形と比の定理で DE平行BCならばAD：AB＝DE：BC というものの逆が成り立たないのは何故なんでしょうか。 教科書も参考書も当たり前すぎるのか反例の記載がないんですが 気になったので誰か教えて 頂けると嬉しいです. 中線定理の3通りの証明 | 高校数学の美しい物語. 中線定理の証明の方針. 教科書にも載っている中線定理ですが，正弦定理や余弦定理などの花型公式と比べるとやや地味な感じがします。. 現物 分配 と は

親子 で 英会話 本しかし，中線定理は様々な手法で証明できるので， 図形の証明問題のよい題材です。. このページでは中線定理の証明 . 三角形の定理や性質 | わかる数学. 三平方の定理. 別名：ピタゴラスの定理. 三角形において、成り立つ公式です。.

∠C = 90∘ a2 + b2 = c2. 角と辺の関係. ABCで∠A, ∠B, ∠Cの対辺の長さを,それぞれa, b, c とするとき、次の事が成り立つ。. ∠C < 90∘ → a2 +b2 < c2 ∠C = 90∘ → a2 +b2 = c2 ∠C > 90∘ → a2 . 三角形の相似条件と相似比・面積比の関係についてわかりやすく解説!. 以下の図のようにAB＝5、AC＝4、BC＝7の三角形ABCとAB＝10、AC＝8、BC＝14の三角形DEFがあったとき、三角形ABCと三角形DEFは3辺の比がすべて等しいので相似と言えます。. 辺の比＝5：10＝1：2になっているので、相似比は1：2となるわけです。. また、面積比は面積 . 角の二等分線に関する重要な3つの公式 | 高校数学の美しい物語. 公式1は有名な辺の比の公式で教科書にも載っています。覚えましょう。 公式2は暗記する必要はありませんが，導出方法は覚えておくとよいです。 公式3はスチュワートの定理の特殊な形です。おもしろいですし，応用例も多いです。. 【高校数学】"内角の二等分線と比"の公式とその証明 | enggy. まとめ記事に戻る. 【高校数学】数Aの公式一覧とその証明まとめ!. "内角の二等分線と比"の公式とその証明です!. 内角の二等分線と比 公式 内角の二等分線と比 ∠Aの二等分線とBCの交点をPとすると (BP：PC＝AB：AC) 証明① 三角形の相似による証明 証明 . 角の二等分線とは？外角・内角の定理や性質をわかりやすく解説 | 受験辞典. 注目する角をはさむ 2 辺と、角の二等分線によって分けられた底辺の比は一致し、これを「角の二等分線の定理」といいます。. 内角でも外角でも同じ関係式ですが、二等分線と底辺との交点 D は、内角の二等分線の場合は ABC の中に、外角の二等分線の場合 . 三平方の定理(ピタゴラスの定理)と三角比の導入 | 教遊者. 残り 1 辺を三平方の定理を使って求めると、. 【三平方の定理】. 1 2 + x 2 = 2 2 これを解いて、 x = 3. よって、その辺の比は、 1: 2: 3 となります。. ② 45 °, 45 °, 90 ° POINT：正方形の半分. 正方形の 1 辺の長さを①とすると、 1 辺は同じ長さなので①となります . 円周角の定理とその逆の証明 | 高校数学マスター. 円周角の定理とその逆について、詳しい証明を行います。数学Aの教科書では、円周角の定理とその逆は中学で学ぶ事柄の復習として証明なしで紹介されています。ただ、証明抜きの事実として用いてきた人も多いのではないでしょうか。円周角の定理とその逆は、円に関係する多くの命題で . チェバの定理とその逆|思考力を鍛える数学 - 思考力を鍛える数学. ホーム >> 平面図形 >> チェバの定理とその逆 2017/4/11 平面図形三角形の頂点を通る $3$ 直線が $1$ 点で交わるとき，次のチェバの定理が成り立ちます．チェバの定理： $ ABC$ の頂点 $. 中点連結定理とは？三角形・台形・四角形の証明をわかりやすく解説 | 個別指導塾wam.

こんにちは!. 個別指導WAMです (^^) 今回は、『中点連結定理とは？. 三角形・台形・四角形の証明をわかりやすく解説』についてご紹介します。. 皆さんは「中点連結定理」を覚えていますか？. あるいは、これから学校で習うという人もいるかもしれません . 「中点連結定理」とは？三角形の中点連結定理の証明をわかりやすく解説 - 中3数学｜ゆみねこの教科書. 中点連結定理とは. 「中点連結定理」とは、「三角形と比の定理」の少し特殊なバージョンだと思っておけばOKだよ。. 名前の通り「中点」を「連結」させたときの性質のことだよ。. ちなみに、図形の中点を連結させたときの定理なので、今回紹介する三角 . ピタゴラスの定理 - Wikipedia. 日本の明治時代の中等学校の教科書では「ピュタゴラスの定理」と呼ばれていた。 現在、ピタゴラスの定理は「三平方の定理」とも呼ばれているが、「三平方の定理」と呼ばれるようになったのは1942年（昭和17年）の太平洋戦争開始後のことである 。. 初めて の 恋 が 終わる 時 楽譜

勉強 不安 手 につか ない比の相等 | 比が等しいことの定義【三角形の相似も利用する公式の証明】 | 岩井の数学ブログ. AB ÷ DE と BC ÷ EF の値が、相似な三角形だから同じ値になっています。. そのため、. AB : DE = BC : EF と二つの比が等しいと結論づける流れです。. 被せ た 歯 が 痛い セラミック

み また ん 霧島 パノラマ ま ら そん比が等しいということを示すときに、割り算の値（比の値）を計算して同じだから比が等しいと示す方法と合わせ . 三角形の内心について知っておきたい知識まとめ | 理系ラボ. 愛犬 の 友 社

こち亀 纏 と 結婚東大塾長の山田です。 このページでは、「三角形の内心」について解説します。 三角形の内心の定理と、その証明を、イラスト付きで丁寧にわかりやすく解説していきます。 また、さいごには三角形の内心の定理を利用する練習問題も用意しているので、ぜひ最. 相似条件とは？三角形の相似条件はなぜ3つなの？【証明問題アリ】 | 遊ぶ数学. 中点連結定理については「中点連結定理とは？逆の証明や平行四辺形の問題もわかりやすく解説!」の記事で詳しく解説しております。 スポンサーリンク 相似比から面積比・体積比. 最後は「相似条件の応用」というより「相似比の応用」です。. 中点連結定理 - Wikipedia. 中点連結定理。辺 mn と bc の長さの比は 1:2 であり、2 . このことから、一般に中点連結定理の逆と呼ばれる定理は、a. の内容であり、より簡単に「三角形の底辺を除く一辺の中点から、底辺の平行線を引くと、残りの辺の中点を通る」と表現される。. 円周角の定理の難問【円や半円の問題】中学数学～高校入試 - 坂田先生のブログ. 円周角の定理を使う円や半円の問題｜中学数学の定期テスト対策 中学数学の定期テスト対策の範囲です。 円周角の定理を使う円や半円の問題｜高校入試レベルの難問まで 三平方の定理や面積比などもからめた、高校入試で見かける問題です。. 二等辺三角形になる条件「二等辺三角形の証明」（逆と反例とは？） - 中2数学｜ゆみねこの教科書. 中学2年生の数学で学習する「二等辺三角形になるための条件」について、二等辺三角形になるためにはどんな条件が必要なのか？を「逆」と「反例」の考え方を解説しながら説明。二等辺三角形の証明問題の解き方を説明しています。. 【高校数学】"外角の二等分線と比"の公式とその証明 | enggy. まとめ記事に戻る. 【高校数学】数Aの公式一覧とその証明まとめ!. "外角の二等分線と比"の公式とその証明です!. 外角の二等分線と比 公式 外角の二等分線と比 点Aの外角の二等分線とBCの延長との交点をQとすると (BQ：QC＝AB：AC) 証明① 三角形の相似 . 中2数学：逆（仮定と結論の入れ替え、反例の示し方） | 授業わかるーの byナオドット先生｜中学数学のわかりやすい解説サイト. だから、逆にした文章が 成り立つときと成り立たないとき の両方があるんだ。 ①逆が成り立つとき 「三角形の3辺の長さが全て等しいならば、正三角形である。」 これの逆は 「正三角形ならば、三角形の3辺の長さが全て等しい。」 「逆」は、 成立する。. 【高校数学Ⅰ】正弦定理（円周角の定理と三角比の融合）の証明と利用 | 受験の月. シー ランド ピュー ノ どこに 売っ てる

線香 どこで 買う高校数学Ⅰ 三角比と図形の計量. 正弦定理（円周角の定理と三角比の融合）の証明と利用. 正弦定理（円周角の定理と三角比の融合）の証明と利用. 2019.06.23. 検索用コード. 中学で円周角の定理を学習したが, 角度が等しいという以上の活用ができなかった . 三角関数の合成 | おいしい数学. 以上のように2通り(どちらも本質は同じ)方法があります． 2通りあるので，教員や講師によって教え方がバラバラで(当然2通り教える場合もある)，生徒の方も解き方がばらけ易く混乱しやすいというのが苦手な人が多い原因だと思います．. 三平方の定理（ピタゴラスの定理）の公式と計算方法 ｜ Hatsudy：総合学習サイト. 中学数学で学ぶ内容として三平方の定理（ピタゴラスの定理）があります。長さの分からない辺があったとしても、三平方の定理を使うことで長さを計算できるようになります。 三平方の定理を理解するためには、平方根について既に学んでい …. 【高校数学Ⅰ】中線定理(パップスの定理)とスチュワートの定理の三角比による証明 | 受験の月. 中線定理は, パップスの定理とも呼ばれる. 座標平面 (数II})やベクトル (数 B)による証明が自然な気もするが, ここでは三角比を利用する. {2つの三角形にそれぞれ余弦定理を適用して整理し, 2式の両辺を足す}ことで導かれる. 2式の両辺を足すことで {cosθが . 中点連結定理とは？証明や問題の解き方をわかりやすく解説! | 受験辞典. この記事では、「中点連結定理」の意味や証明、定理の逆についてわかりやすく解説していきます。. また、問題の解き方もていねいに解説していくので、ぜひこの記事を通してマスターしてくださいね!. 目次 [ 非表示] 中点連結定理とは？. 中点連結定理 . 【高校数学a】三角形の内角・外角の二等分線と辺の比の関係とその証明 | 受験の月. 三角形の内角・外角の二等分線と辺の比の関係とその証明. 2020.11.15. 検索用コード. 三角形の角の二等分線と辺の比Aの二等分線と辺BCの交点Pは, 辺BCを 直線APに平行な直線を点Cを通るように引き, 直線ABの交点をDとする (右図). ffftp sftp で 接続

マナカ スマホ で 使える(同位角), (錯角)}$ 仮定よりは . タレスの定理の逆 - A4の宇宙. タレスの定理の逆を証明する。 すなわち、∠cを直角とする直角三角形abcと、頂点abcを通る円を考えるとき、図のように辺abが円の直径になることを示す。 証明 辺abの中点をpとし、点pから∠cに補助線を引く。 pcと平行に点aから新たな補助線を引く。辺bcを延長し、交点をqとする。. 【数学Ⅱ】三角関数の公式まとめ（加法定理・変換・合成） | 理系ラボ. 東大塾長の山田です。 このページでは、「三角関数の公式（性質）」をすべてまとめています。 ぜひ勉強の参考にしてください! 1. 三角関数の相互関係 ( sin theta, cos theta, tan theta. 角の二等分線の性質の逆について。三角形ABCにおいて、角Aの二等. - Yahoo!知恵袋. 1 回答. 忌引き の 人 へ の メール

角の二等分線の性質の逆について。. 三角形ABCにおいて、角Aの二等分線とBCの交点をMとしたとき、AB:AC＝BM:MCが成り立つ。. この性質の逆、AB:AC＝BM:MCが成り立つときAMはAの二等分線である。. ということが証明できません。. どなたか教えてください. 高校数学i 三角比と図形の計量 基本事項まとめ（公式・定理・パターン・注意点・裏技） | 受験の月. 高校数学Ⅰ 三角比と図形の計量. 定期試験・大学入試に特化した問題と解説。. 三角比分野のパターンを基本から応用、裏技までを網羅する。. examist.jp. 高校数学 分野別基本事項まとめ（試験直前最終確認用）. 三角比と図形の計量分野の試験直前の最終確認 . 接弦定理とは？証明や定理の逆、問題の解き方を解説! | 受験辞典. 円周角の定理「(1) つの弧に対する円周角の大きさは等しい」より、円周角は自由な位置にとれるので、直角三角形をつくって直角をうまく利用するのがポイントです。. 接線と弦が作る角が、(i) 鋭角、(ii) 直角、(iii) 鈍角になる場合の (3) 通りに分けてそれぞれ証明します。. 「円周角の定理の逆」とは？ 証明と問題の解き方をわかりやすく解説のpdfを無料ダウンロード｜ゆみねこの教科書. 証明と問題の解き方をわかりやすく解説のPDFを無料ダウンロード｜ゆみねこの教科書. 「円周角の定理の逆」とは？. 証明と問題の解き方をわかりやすく解説のPDFをダウンロード. ※このPDFは 8枚 で構成されております。. 方べきの定理とその逆の証明 | 高校数学マスター. 方べきの定理とその逆の証明は、初めて高校数学を学習する生徒にとっては根拠をたどるのが難しい内容だと思います。そこで、このページでは、方べきの定理とその逆をきちんと根拠を明示しながら丁寧に証明していきます。その過程で、四角形が円に内接する条件、接弦定理の逆、なども . 直角三角形とは？定義や定理、辺の長さの比、合同条件 | 受験辞典. この記事では、「直角三角形」の定義や合同条件、重要な辺の長さの比について解説していきます。. また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね!. 目次 [ 非表示] 直角三角形の定義. 直角三角形の定理（三平方の定理 . 【中3数学】三平方の定理とは？テストで役立つ辺の比7パターンと公式・証明を紹介 | 塾 テラコヤプラス by Ameba. 【中3数学】「三平方の定理」は、直角三角形の辺の長さを求める時に使える、シンプルで基本的な定理。別名「ピタゴラスの定理」ともいいます。三平方の定理は高校入試の定番問題のため、マスターしておけば得点につながります。そこで、この記事では「三平方の定理」を理解するための . 三平方の定理を慶應生が超わかりやすく解説!公式・証明・計算問題付き｜高校生向け受験応援メディア「受験のミカタ」. 三平方の定理が、数学が苦手な人でも必ず理解できます。公式の説明だけでなく、三平方の定理の公式の証明、計算方法と解き方、暗記すべき比と角度、計算問題まで紹介しています。この記事だけで三平方の定理について充実の内容です。. 三角形の重心(3中線が1点で交わることの証明)｜スライドで学ぶ高校数学 | ひまわり数学教室. 中学校の範囲. 1. 円周角の定理. 2. 円周角の定理の逆. 三角形には3本の中線が引けて、それらが1点で交わることが知られています。. これが三角形の重心です。. ここではなぜ3本の線分が1点で交わることになるのかを丁寧に説明していきます。